Weighted Least Squares Regression
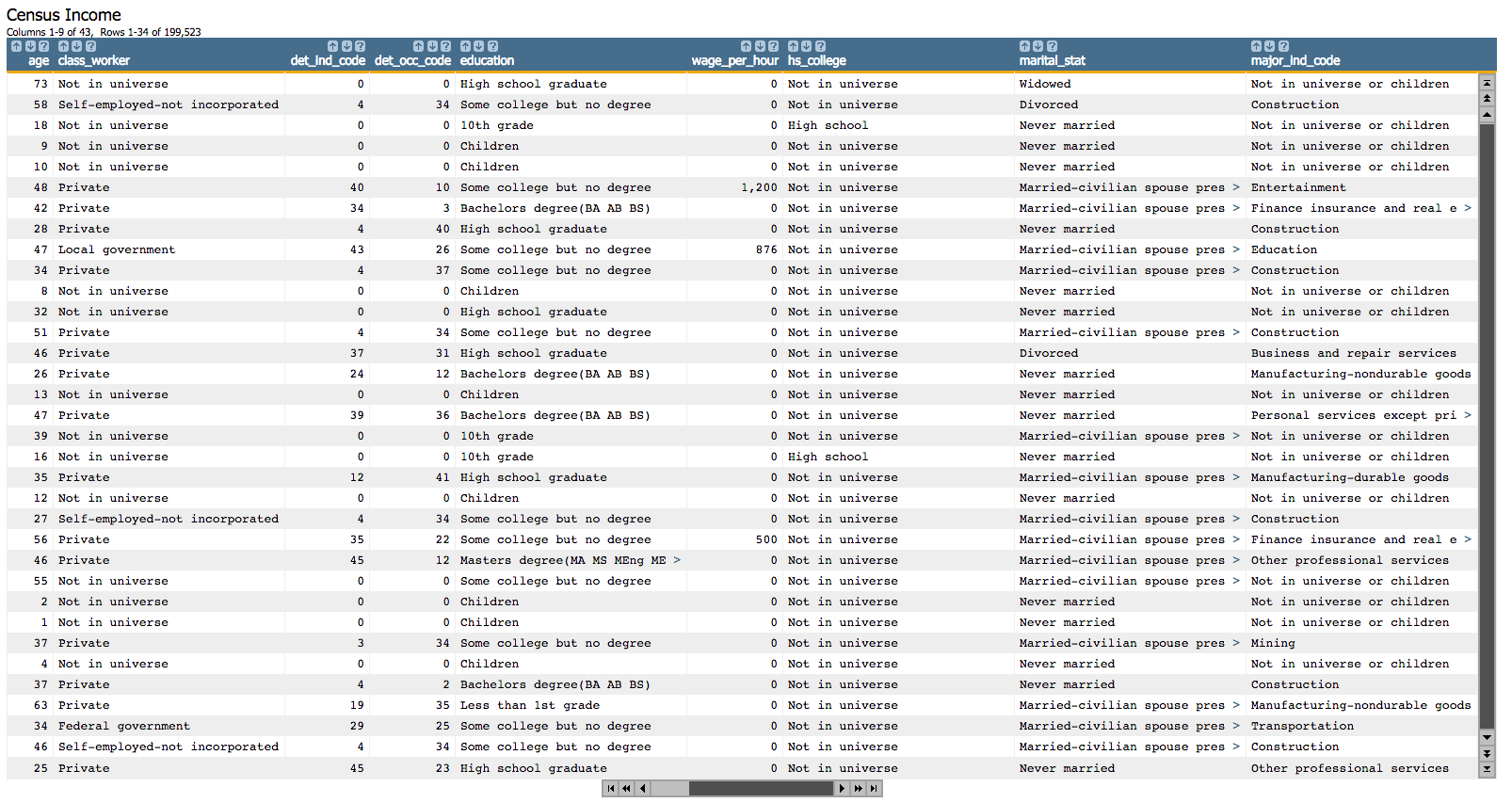
In this example, a weighted least squares regression is applied to a data set containing weighted census data to show the relationship between both the age and education level of a worker and that person's income.
The weighted least squares regression, using the 1010data function
g_wlsq(G;S;Y;W;XX), is applied to the
Census Income Data Set, which contains weighted census data extracted from
the 1994 and 1995 Current Population Surveys conducted by the U.S. Census Bureau.
ageedu_year
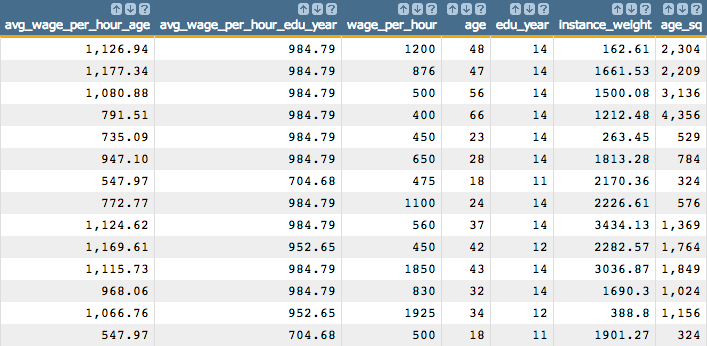
It also uses the square of the age, which we calculate in this tutorial.
For the weight, we will use the column instance_weight, which
represents how each person in the survey relates demographically to the overall
population.
As a response, the column wage_per_hour is used.
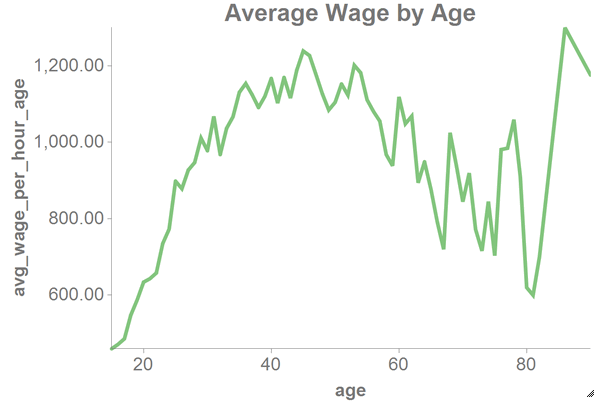
After applying the weighted least squares technique, the results show the linear relationship between both the age and education level of the worker and that person's wages per hour.
- Select only those rows where wages are not equal to zero, since we only want to do the regression for those people who have a job.
- Check the relationship of each of the predictors to the response and adjust for those that have a quadratic form.
- Fit the model on the three predictors and the response.
- Obtain the predicted value of the linear model.
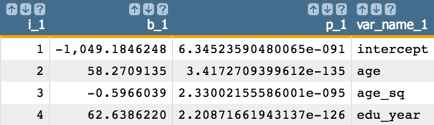
- Obtain the coefficients of the linear model.
- Obtain the p-values of the coefficients.
- Obtain various statistics for the model such as the degrees of freedom, residual sum of squares, mean squared error, and number of observations.
- Calculate the AIC.
- Visualize the results of the weighted least squares regression by plotting the age against both the wages per hour and the predicted value of the linear model.
If you want to see how to calculate the standard error of the coefficients or how to chart the residual plot, QQ plot, PP plot, or how to plot the predicted value against the original response, see the Least Squares Regression tutorial.