Principal Component Analysis

In this example, a principal component analysis is used as a dimension reduction technique to determine the principal components of a data set containing bank marketing information. These principal components are then used in a logistic regression to predict whether or not a customer subscribed for a term deposit.

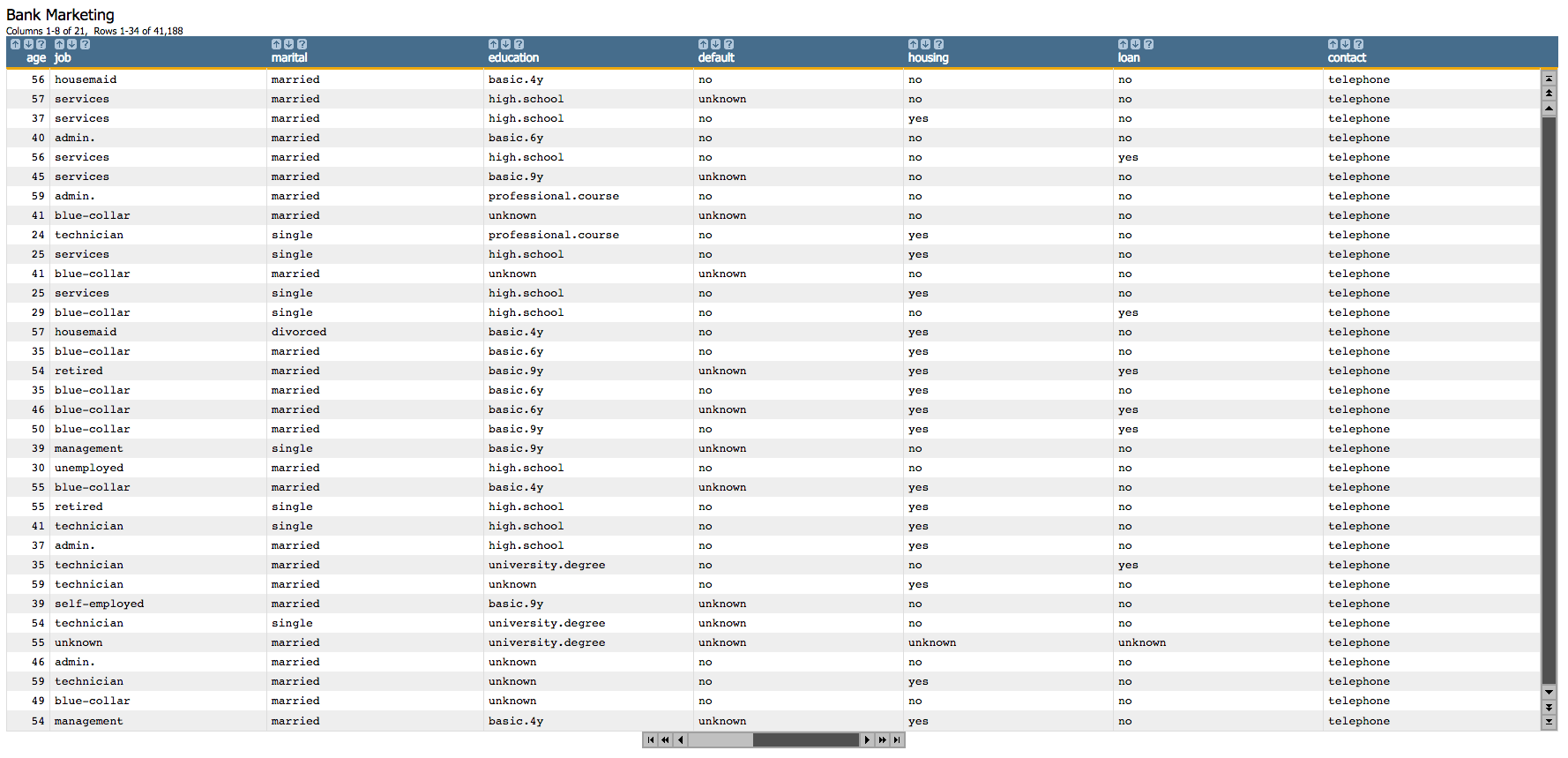
The principal component analysis, using the 1010data function g_pca(G;S;XX;Z), will be performed on the Bank Marketing Data Set, which was used in the Logistic Regression example. This data set contains information related to a campaign by a Portuguese banking institution to get its customers to subscribe for a term deposit.

The principal component analysis uses the following 10 variables in that data set:

age
duration
previous
empvarrate
housing
default
loan
poutcome
job
marital

This analysis will follow the following steps:

Prepare the data by creating dummy variables for each of the categorial columns (since we cannot use textual data to build our model).
Run the principal component analysis (on the continuous variables in the original data set and the dummy variables that we created) using the correlation matrix of the data.
Obtain the principal components.
Extract the eigenvalues and eigenvectors from the PCA model and calculate the cumulative sum of the eigenvalues to show their distribution.
Chart both the distribution of explained variance in the PCA and the cumulative distribution of the variance.
Obtain various model statistics, including the number of observations, the mean value of a specific column, and the standard deviation of a specific column.
Divide the data into a training set and a test set.
Run the logistic regression on the training data set based on the first three principal components.
Obtain the predicted probability that a customer has subscribed for a term deposit.
Create a cumulative gains chart and calculate the area under the curve (AUC) for the test data.
Chart the logistic curve for both the training and test data.

The results of the logistic regression should be similar to those found in the Logistic Regression example, depending on the number of principal components used.

Open the Bank Marketing data set (pub.demo.mleg.uci.bankmarketing).

Since we cannot use textual data in our analysis, we first create dummy variables for each of the categorial columns.

<willbe name="yy" value="y='yes'"/>
<willbe name="hsng" value="housing='yes'"/>
<willbe name="h_unk" value="housing='unknown'"/>
<willbe name="def" value="default='yes'"/>
<willbe name="d_unk" value="default='unknown'"/>
<willbe name="loans" value="loan='yes'"/>
<willbe name="l_unk" value="loan='unknown'"/>
<willbe name="nonxst" value="poutcome='nonexistent'"/>
<willbe name="succ" value="poutcome='success'"/>
<willbe name="blue" value="job='blue-collar'"/>
<willbe name="tech" value="job='technician'"/>
<willbe name="j_unk" value="job='unknown'"/>
<willbe name="svcs" value="job='services'"/>
<willbe name="mgmt" value="job='management'"/>
<willbe name="ret" value="job='retired'"/>
<willbe name="entr" value="job='entrepreneur'"/>
<willbe name="self" value="job='self-employed'"/>
<willbe name="maid" value="job='housemaid'"/>
<willbe name="unemp" value="job='unemployed'"/>
<willbe name="stud" value="job='student'"/>
<willbe name="marr" value="marital='married'"/>
<willbe name="sgl" value="marital='single'"/>
<willbe name="m_unk" value="marital='unknown'"/>

These <willbe> operations create a computed column for each of the categories, where a 1 in the column indicates that the category is true for that row. For instance, in the following screenshot, the rows where hsng=1 indicate that the client had a housing loan (i.e., housing='yes' in the original table), and the rows where h_unk=1 indicate that it is unknown if the client had a housing loan (i.e., housing='unknown').

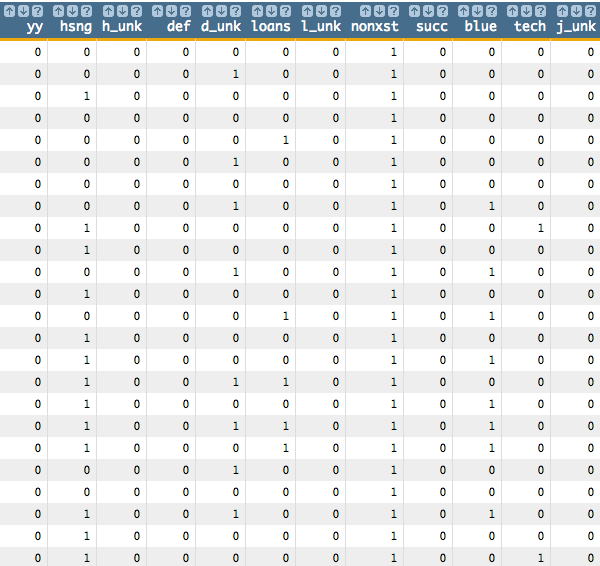
See Dummy Variables for a list of the dummy variables used here and their meanings.

Using g_pca(G;S;XX;Z), we run the principal component analysis on the continuous variables in the original data set and the dummy variables that we created. We use the corr method, which means we standardize our data first.
```
<note>COMPUTE PCA MODEL WITH 26 VARIABLES</note>
<willbe name="model_pca" value="g_pca(;;age duration previous empvarrate 
hsng h_unk def d_unk loans l_unk nonxst succ blue tech j_unk svcs mgmt 
ret entr self maid unemp stud marr sgl m_unk;'method''corr')"/>
```
This creates a column named model_pca that contains the results of the principal component analysis:

Clicking on the > opens a window containing a summary of the principal component analysis:

We can then obtain the principal components by using the score(XX;M;Z) function.

<note>OBTAIN FIRST PRINCIPAL COMPONENT</note>
<willbe name="pc1" value="score(age duration previous empvarrate 
hsng h_unk def d_unk loans l_unk nonxst succ blue tech j_unk svcs 
mgmt ret entr self maid unemp stud marr sgl m_unk; model_pca ; 1)"/>
<note>OBTAIN SECOND PRINCIPAL COMPONENT</note>
<willbe name="pc2" value="score(age duration previous empvarrate 
hsng h_unk def d_unk loans l_unk nonxst succ blue tech j_unk svcs 
mgmt ret entr self maid unemp stud marr sgl m_unk; model_pca ; 2)"/>
<note>OBTAIN THIRD PRINCIPAL COMPONENT</note>
<willbe name="pc3" value="score(age duration previous empvarrate 
hsng h_unk def d_unk loans l_unk nonxst succ blue tech j_unk svcs 
mgmt ret entr self maid unemp stud marr sgl m_unk; model_pca ; 3)"/>

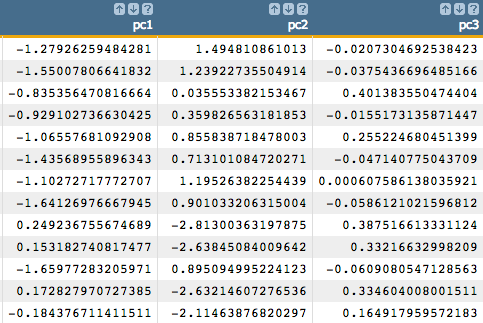
Note: For our example, we extract the first three principal components. However, we could use the distribution of the eigenvalues to more precisely determine the number of principal components we should use in the logistic regression in order to obtain the best results. We see how to do that in the following steps.

Let's use the param(M;P;I) function to extract the eigenvalues and eigenvectors from the PCA model. Note that we extract one value at a time.

<willbe name="eigen_value1" value="param(model_pca;'evals';1)"/>
<willbe name="eigen_value2" value="param(model_pca;'evals';2)"/>
<willbe name="eigen_vector_1_elem_1" value="param(model_pca;'evecs';1 1)"/>
<willbe name="eigen_vector_1_elem_2" value="param(model_pca;'evecs';1 2)"/>

Alternatively, we can calculate the eigenvalues for the PCA model all at once in one column and then calculate their cumulative sum to show their distribution. This distribution can then be used to determine how many principal components to use in the logistic regression.

Note: The number of eigenvalues we extract from the PCA model corresponds to the number of variables in our analysis. So, for our example, we extract 26 eigenvalues.
```
<note>CALCULATE EIGENVALUES IN ONE COLUMN</note>
<willbe name="temp_i" value="mod(i_(1);26)"/>
<willbe name="i" value="if(temp_i=0;26;temp_i)"/>
<willbe name="eigen_value" value="param(model_pca;'evals';i)"/>
<note>VARIANCE DISTRIBUTION FOR EIGENVALUE</note>
<willbe name="indicator" value="i_(1)<=26"/>
<willbe name="cum_variance" value="g_cumsum(;indicator;;eigen_value)/g_sum(;indicator;eigen_value)"/>
```
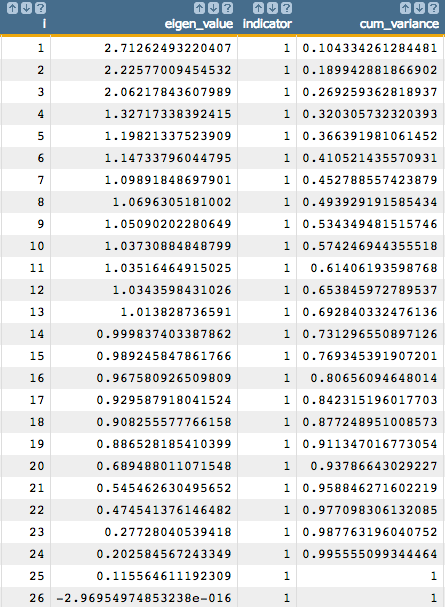
Using this information, we can determine how many principal components we should use based on the value in the cum_variance column. We can see that if we want to include 80% of the information from our original data, we need to use at least 16 principal components.
To visualize the distribution of explained variance in the PCA, use the 1010data Chart Builder.
1. Click Chart > Bar.
2. Drag the eigen_value column to the DATA (BARS) area.
3. Click Update.
You should see a chart similar to the following:
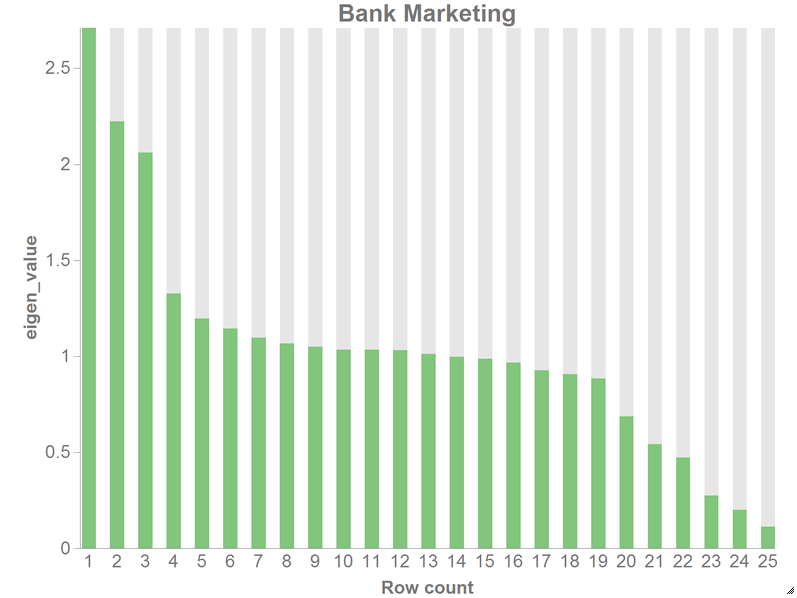
You can also plot the cumulative distribution of the variance.
1. Click Chart > Scatter.
2. Drag the cum_variance column to the DATA (Y-AXIS) area.
3. Under the Settings section, enter 26 for X-Range (max).
4. Click Update.
You should see a chart similar to the following:

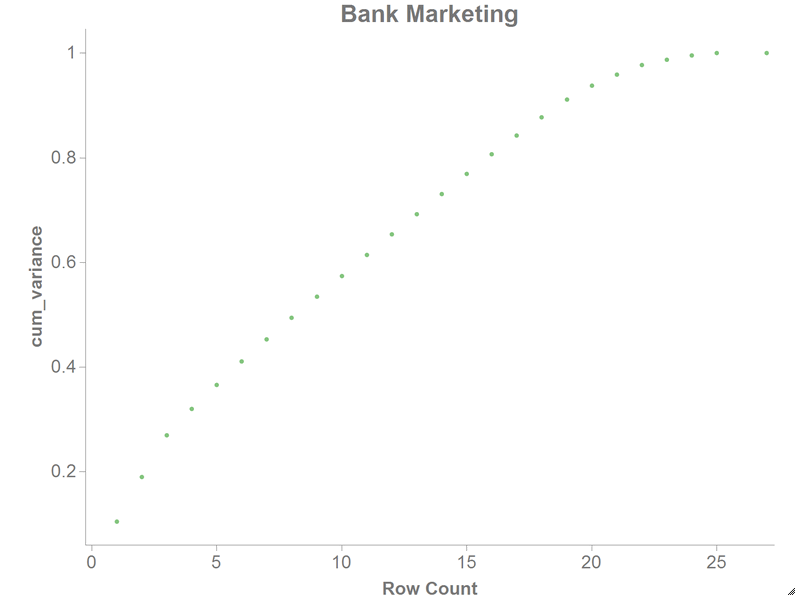
We can use the param(M;P;I) function to obtain various model statistics, depending on our analytical purposes. Some of these statistics include the number of observations, the mean value of a specific column, and the standard deviation of a specific column.

<note>OBTAIN VARIOUS MODEL STATISTICS</note>
<willbe name="num_observations" value="param(model_pca;'valcnt';)"/>
<willbe name="mean_1" value="param(model_pca;'center';1)"/>
<willbe name="mean_2" value="param(model_pca;'center';2)"/>
<willbe name="std_dev_1" value="param(model_pca;'scale';1)"/>
<willbe name="std_dev_2" value="param(model_pca;'scale';2)"/>

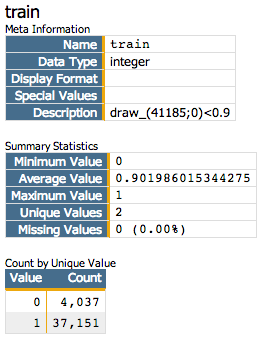
Next, we want to create a column that we will use to separate training data and test data. We want to use 90% of our data as training data.
```
<note>SELECT TRAINING DATA</note>
<willbe name="train" value="draw_(41185;0)<0.9"/>
<willbe name="test" value="train<>1"/>
```
For demonstration purposes, we run the logistic model (g_logreg(G;S;Y;XX;Z)) using just the first three principal components we stored earlier (instead of the 26 variables we used in the Logistic Regression example) and using the column yy as a response, which is 1 if a customer has subscribed for a term deposit.

We use the train column from the previous step as the second parameter of the g_logreg(G;S;Y;XX;Z) function. The train column will act as a selector, so that our function will only train 90% of the data. We also specify options for the Z parameter that control convergence criteria.
```
<note>COMPUTE LOGREG USING THE FIRST 3 PRINCIPAL COMPONENTS</note>
<willbe name="model" value="g_logreg(;train;yy;1 pc1 pc2 pc3;'cgdeveps' 0.0000001 'lreps' 0.000000001)"/>
```
Note: The first element of XX must be the special value 1 for the constant (intercept) term in the linear model.
This creates a column named model that contains the results of the logistic regression:

Clicking on the > opens a window containing a summary of the model output:
We can then use the score(XX;M;Z) function to obtain the predicted probability (prob_score) returned by the logistic model, which in our example represents the probability a person subscribed for a term deposit.
```
<note>OBTAIN MODEL SCORE WITH SCORE FUNCTION</note>
<willbe name="prob_score" value="score(1 pc1 pc2 pc3;model;)"/>
```
To create the cumulative gains chart and calculate the area under the curve, clone the current tab and follow the steps in Chart cumulative gains and calculate the AUC in the cloned tab.

You should see results similar to the following:

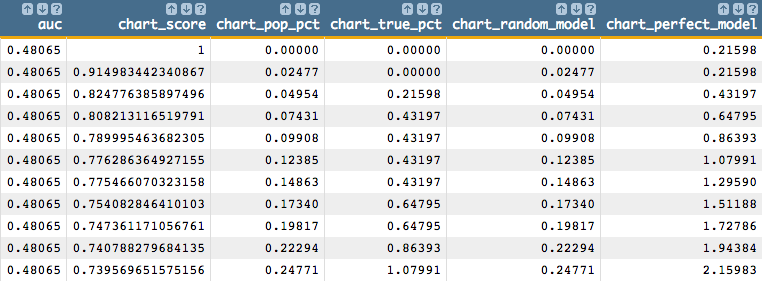
You should also see a chart that looks like the one below:
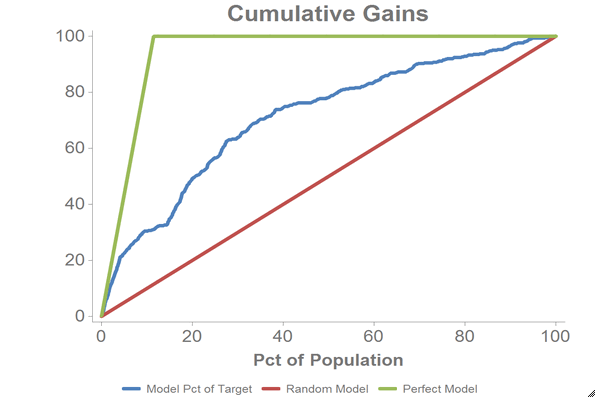
We can also calculate the logit of the predicted probability (prob_score), which we can use for purposes of further analysis such as visualization.

Note: Perform the remaining steps in the original tab, not the cloned tab.
```
<willbe name="z_estimate" value="loge(prob_score / (1-prob_score))"/>
```
We can chart the logistic curve for both the training and test data using the 1010data Chart Builder.

Let's chart the results for our training data:
1. Create computed columns that contain the prob_score and z_estimate for just the training data.
```
<willbe name="prob_score_train" value="prob_score*train"/>
<willbe name="z_estimate_train" value="z_estimate*train"/>
```
2. Click Chart > Scatter.
3. Drag the z_estimate_train column to the DATA (X-AXIS) area.
4. Drag the prob_score_train and yy columns to the DATA (Y-AXIS) area.
5. Change X-Range (max) to 3.5.
6. Click Update.
Let's chart the results for our test data:
1. Create computed columns that contain the prob_score and z_estimate for just the test data.
```
<willbe name="prob_score_test" value="prob_score*test"/>
<willbe name="z_estimate_test" value="z_estimate*test"/>
```
2. Click Chart > Scatter.
3. Drag the z_estimate_test column to the DATA (X-AXIS) area.
4. Drag the prob_score_test and yy columns to the DATA (Y-AXIS) area.
5. Change X-Range (max) to 3.5.
6. Click Update.
The results should look similar to the following charts:

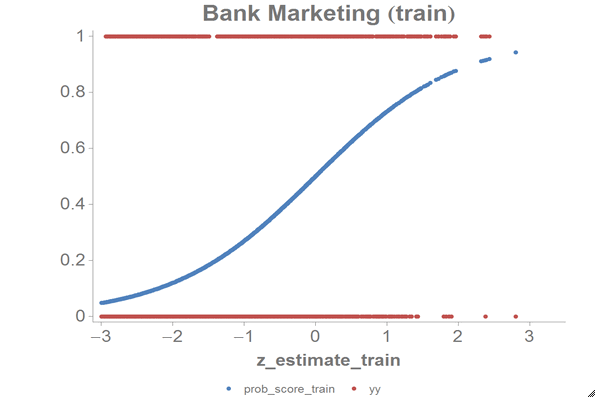
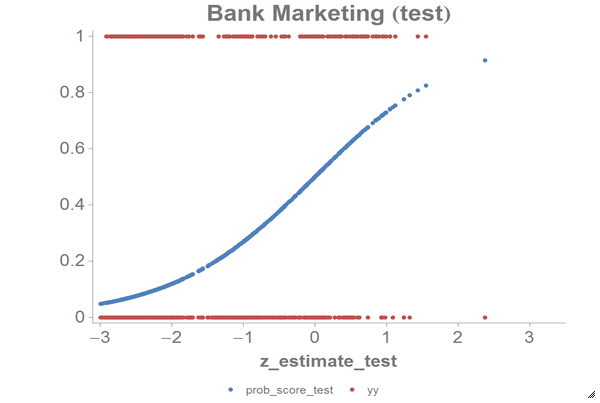
Based on the chart and the error rate that we got, we can see that the PCA model successfully reduces the dimensions of our data as well as the computations for our logistic model. We can compare these results to those we achieved in the Logistic Regression example.