Logistic Regression

In this example, a logistic regression is performed on a data set containing bank marketing information to predict whether or not a customer subscribed for a term deposit.

1. Open the Bank Marketing data set (pub.demo.mleg.uci.bankmarketing).

   

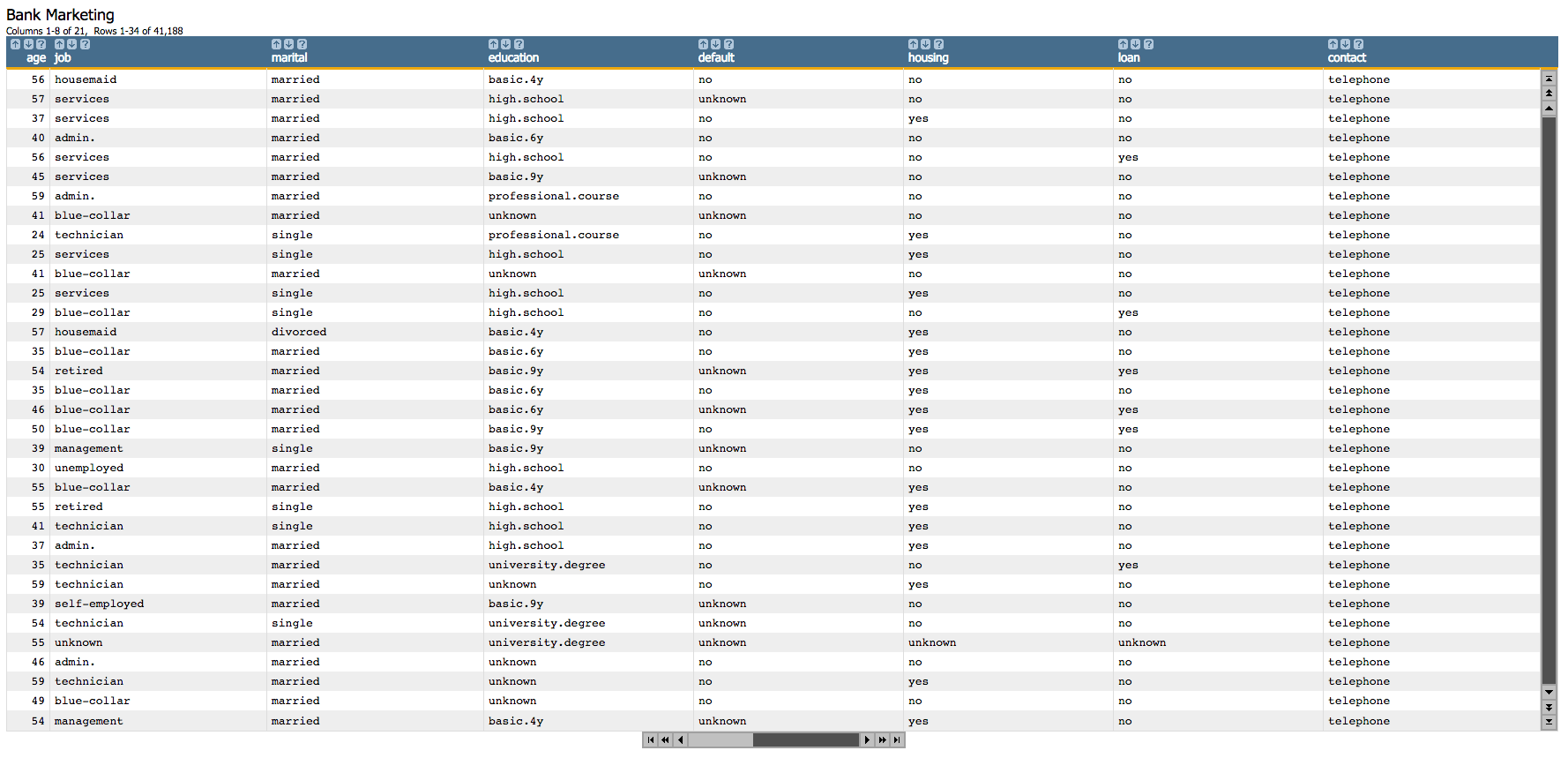
2. Since we cannot use textual data in our analysis, we first create dummy variables for each of the categorial columns.

   <willbe name="yy" value="y='yes'"/>
   <willbe name="hsng" value="housing='yes'"/>
   <willbe name="h_unk" value="housing='unknown'"/>
   <willbe name="def" value="default='yes'"/>
   <willbe name="d_unk" value="default='unknown'"/>
   <willbe name="loans" value="loan='yes'"/>
   <willbe name="l_unk" value="loan='unknown'"/>
   <willbe name="nonxst" value="poutcome='nonexistent'"/>
   <willbe name="succ" value="poutcome='success'"/>
   <willbe name="blue" value="job='blue-collar'"/>
   <willbe name="tech" value="job='technician'"/>
   <willbe name="j_unk" value="job='unknown'"/>
   <willbe name="svcs" value="job='services'"/>
   <willbe name="mgmt" value="job='management'"/>
   <willbe name="ret" value="job='retired'"/>
   <willbe name="entr" value="job='entrepreneur'"/>
   <willbe name="self" value="job='self-employed'"/>
   <willbe name="maid" value="job='housemaid'"/>
   <willbe name="unemp" value="job='unemployed'"/>
   <willbe name="stud" value="job='student'"/>
   <willbe name="marr" value="marital='married'"/>
   <willbe name="sgl" value="marital='single'"/>
   <willbe name="m_unk" value="marital='unknown'"/>

   These <willbe> operations create a computed column for each of the categories, where a 1 in the column indicates that the category is true for that row. For instance, in the following screenshot, the rows where hsng=1 indicate that the client had a housing loan (i.e., housing='yes' in the original table), and the rows where h_unk=1 indicate that it is unknown if the client had a housing loan (i.e., housing='unknown').

   

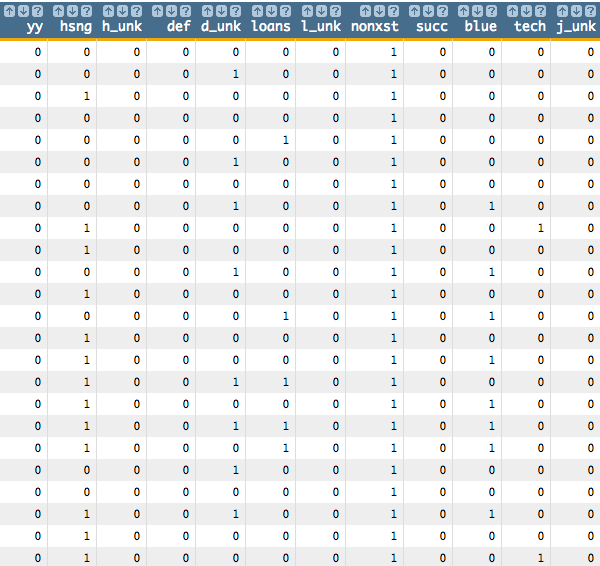
   See Dummy Variables for a list of the dummy variables used here and their meanings.

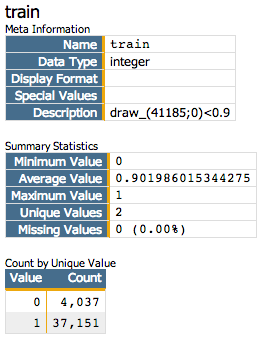
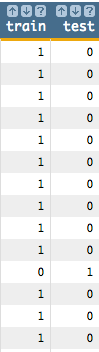
3. Next, we want to create a column that we will use to separate training data and test data. We want to use 90% of our data as training data.

   <note>SELECT TRAINING DATA</note>
   <willbe name="train" value="draw_(41185;0)<0.9"/>
   <willbe name="test" value="train<>1"/>

   

4. Now we run the logistic regression based on the continuous variables in the original data set and the dummy variables that we created. We use the train column from the previous step as the second parameter of the g_logreg(G;S;Y;XX;Z) function. The train column will act as a selector, so that our function will only train 90% of the data. We also specify options for the Z parameter that control convergence criteria.

   <willbe name="model" value="g_logreg(;train;yy;1 age duration 
   previous empvarrate hsng h_unk def d_unk loans l_unk nonxst succ blue 
   tech j_unk svcs mgmt ret entr self maid unemp stud marr sgl m_unk;
   'cgdeveps' 0.0000001 'lreps' 0.000000001)"/>

   Note: The first element of XX must be the special value 1 for the constant (intercept) term in the linear model.

   This creates a column named model that contains the results of the logistic regression:

   

   Clicking on the > opens a window containing a summary of the model output:

   

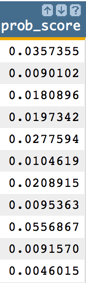
5. We can then use the score(XX;M;Z) function to obtain the predicted probability (prob_score) returned by the logistic model, which in our example represents the probability a person subscribed for a term deposit.

   <note>OBTAIN MODEL SCORE WITH SCORE FUNCTION</note>
   <willbe name="prob_score" value="score(1 age duration previous empvarrate 
   hsng h_unk def d_unk loans l_unk nonxst succ blue tech j_unk svcs mgmt ret 
   entr self maid unemp stud marr sgl m_unk;model;)" format="dec:7"/>

   Note: We specify format="dec:7" so that our results show with 7 decimal places.

   

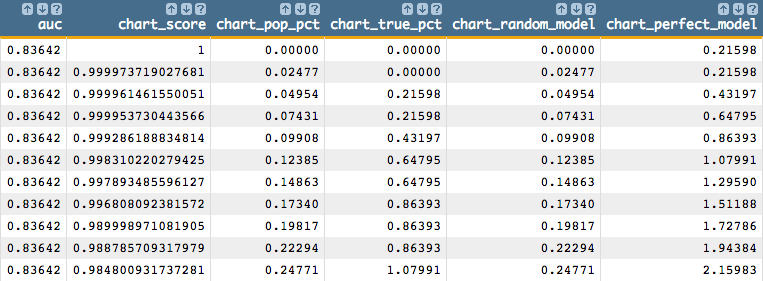
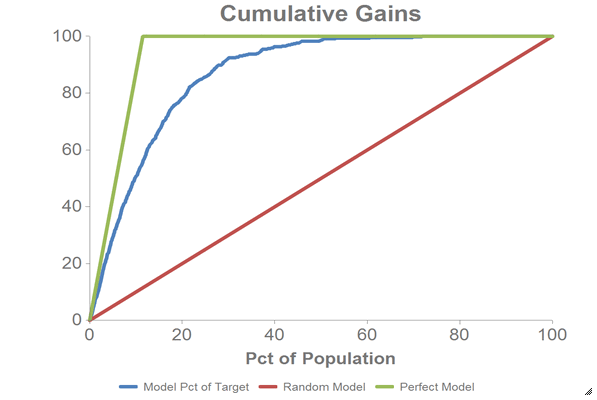
6. To create the cumulative gains chart and calculate the area under the curve, clone the current tab and follow the steps in Chart cumulative gains and calculate the AUC in the cloned tab.

   You should see results similar to the following:

   

   

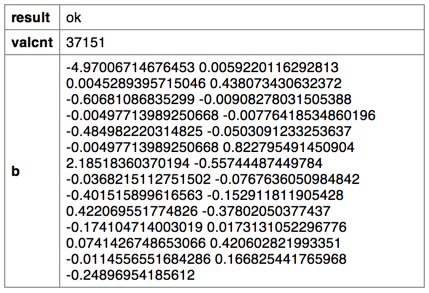
7. To obtain the model coefficients, we can use the param(M;P;I) function. For our example, we will only obtain the parameters for the intercept (b0) and the first three variables (b1, b2, and b3).
   Note: Perform the remaining steps in the original tab, not the cloned tab.

   <willbe name="b0" value="param(model;'b';1)" format="dec:7"/>
   <willbe name="b1" value="param(model;'b';2)" format="dec:7"/>
   <willbe name="b2" value="param(model;'b';3)" format="dec:7"/>
   <willbe name="b3" value="param(model;'b';4)" format="dec:7"/>

   

8. One might also want to obtain coefficients in one column, which can be achieved with the following:

   <note>CALCULATE COEFFICIENTS IN ONE COLUMN</note>
   <willbe name="var_names" value="'intercept,age,duration,previous,
   empvarrate,hsng,h_unk,def,d_unk,loans,l_unk,nonxst,succ,blue,tech,
   j_unk,svcs,mgmt,ret,entr,self,maid,unemp,stud,marr,sgl,m_unk'"/>
   <willbe name="temp_i" value="mod(i_(1);27)"/>
   <willbe name="i" value="if(temp_i=0;27;temp_i)"/>
   <willbe name="b" value="param(model;'b';i)" format="dec:7"/>
   <willbe name="var_name" value="csl_pick(var_names;i)"/>

   

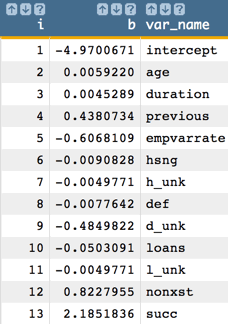
   Note: The number of coefficients we obtain from the model corresponds to the number of variables in our analysis. So, for our example, we obtain 27 coefficients (the intercept and the 26 predictors).
9. To extract logistic regression fit statistics (e.g., deviance, AIC, p-values, z-values, and standard errors), clone the current tab and follow the steps in Extract logistic regression fit statistics in the cloned tab.

   A number of new columns containing the various fit statistics (as well as some intermediary columns that are used in the calculation of the fit statistics) will be added to the table.

   For example, the following columns show deviance and AIC:

   

   The columns below show the standard error, z-values, and p-values for both the intercept (indicated by const in the column names) and the age variable:

   

10. We can also calculate the logit of the predicted probability (prob_score), which we can use for purposes of further analysis such as visualization.
    Note: Perform the remaining steps in the original tab, not the cloned tab.

    <willbe name="z_estimate" value="loge(prob_score / (1-prob_score))" format="dec:7"/>

    

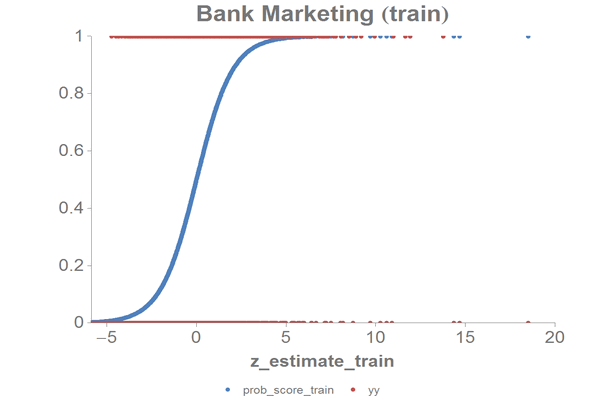
11. We can chart the logistic curve for both the training and test data using the 1010data Chart Builder.

    Let's chart the results for our training data:

    1. Create computed columns that contain the prob_score and z_estimate for just the training data.

       <willbe name="prob_score_train" value="prob_score*train"/>
       <willbe name="z_estimate_train" value="z_estimate*train"/>

    2. Click Chart > Scatter.
    3. Drag the z_estimate_train column to the DATA (X-AXIS) area.
    4. Drag the prob_score_train and yy columns to the DATA (Y-AXIS) area.
    5. Change X-Range (max) to 20.
    6. Click Update.

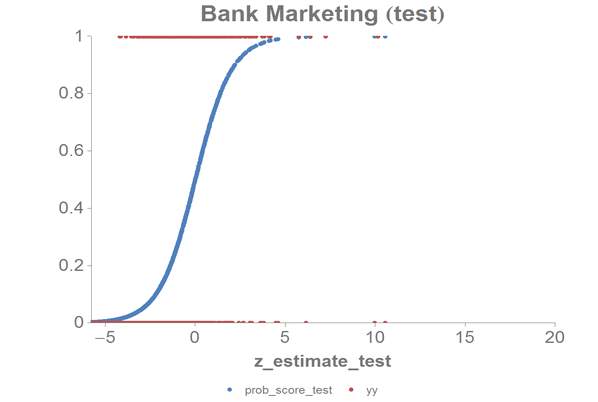
    Let's chart the results for our test data:

    1. Create computed columns that contain the prob_score and z_estimate for just the test data.

       <willbe name="prob_score_test" value="prob_score*test"/>
       <willbe name="z_estimate_test" value="z_estimate*test"/>

    2. Click Chart > Scatter.
    3. Drag the z_estimate_test column to the DATA (X-AXIS) area.
    4. Drag the prob_score_test and yy columns to the DATA (Y-AXIS) area.
    5. Change X-Range (max) to 20.
    6. Click Update.

    The results should look similar to the following charts: