`g_matrix(G;S;O;X;T)`

Returns a matrix model consisting of the data from the specified columns within a given group. (Available as of prod-9)

Function type

Vector only

Syntax

g_matrix(G;S;O;X;T)

Input

Argument	Type	Description
`G`	any	A space- or comma-separated list of column names Rows are in the same group if their values for all of the columns listed in `G` are the same. If `G` is omitted, all rows are considered to be in the same group. If any of the columns listed in `G` contain N/A, the N/A value is considered a valid grouping value.
`S`	integer	The name of a column in which every row evaluates to a 1 or 0, which determines whether or not that row is selected to be included in the calculation If `S` is omitted, all rows will be considered by the function (subject to any prior row selections). If any of the values in `S` are neither 1 nor 0, an error is returned.
`O`	integer	A space- or comma-separated list of column names that determine the row order within a particular group If `O` is omitted, the order is the current display order of the table. If any of the values in `O` are N/A, an error is returned.
`X`	integer or decimal	A space- or comma-separated list of column names
`T`	integer	A scalar value The value of `T` indicates whether or not to return the transpose of the matrix: When `T` is `0` or is not specified, the matrix is returned. When `T` is `1`, the transpose of the matrix is returned.

Return Value

For every row in each group defined by G (and for those rows where S=1, if specified), g_matrix returns a matrix model. The resultant matrices will have the same number of rows as the number of columns specified by the X parameter, and the data in each column of the matrix will correspond to each row in the group specified by G, resulting in an n-row matrix, where n is the number of columns specified by X.

If T=1, the transpose of that matrix is returned, resulting in an n-column matrix.

Example

Consider the following table:

<table cols="name, data_1, data_2, data_3, data_4" title="g_matrix example">
 John,8,0,5,1;
 John,2,0,1,1;
 Mary,3,1,2,2;
 Mary,4,1,2,2;
 John,5,2,3,1
</table>

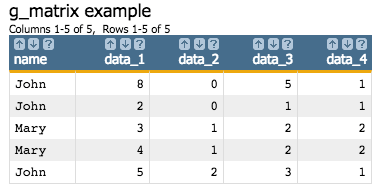
The following call to g_matrix(G;S;O;X;T):

<willbe name="matrix_0" value="g_matrix(name;;;data_1 data_2 data_3 data_4;0)"/>

results in a new column, matrix_0, which contains the matrix model.

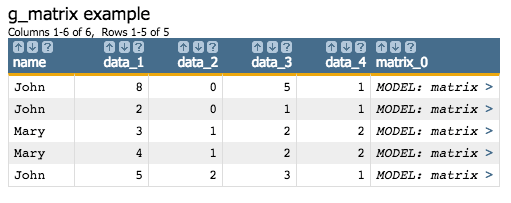
Clicking on the > character in the matrix_0 column for a particular row will open a new window displaying the matrix for the group associated with that row. The matrix will have the same number of rows as the number of columns specified by the X parameter, and the data in each column of the matrix will correspond to each row in the group specified by G.

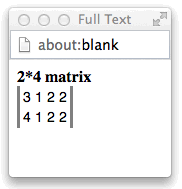
For example, clicking on the > character in the first row of the matrix_0 column displays the matrix for those rows where name is John.

Since the table in this example has four data columns, the resultant matrix has four rows, and since the group where name is John has three rows in the table, the resultant matrix has three columns.

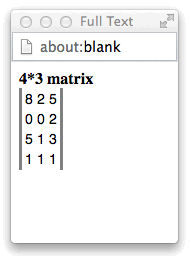
Clicking on any row that has Mary in the name column displays the matrix for those rows:

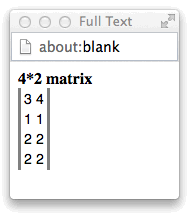
Consider when T is set to 1 in the g_matrix(G;S;O;X;T) call:

<willbe name="matrix_1" value="g_matrix(name;;;data_1 data_2 data_3 data_4;1)"/>

The matrix_1 column will contain the models of the transposed matrices (with respect to those generated when T is set to 0). These transposed matrices will have one column for each of the columns specified by the X parameter, and the data in each row of the matrix will correspond to each row in the group specified by G.

For example, clicking on any row in the matrix_1 column that has Mary in the name column displays the transposed matrix for those rows: