`g_chase(G;S;X;Y;K;D)`

Returns a value indicating whether, in a hierarchy of linked nodes, a particular node is reachable from an initial selection of nodes; or, optionally, the smallest number of hops it would take to reach that node from the initial selection.

Syntax

g_chase(G;S;X;Y;K;D)

Input

Argument	Type	Description
`G`	any	A space- or comma-separated list of column names Rows are in the same group if their values for all of the columns listed in `G` are the same. If `G` is omitted, all rows are considered to be in the same group. If any of the columns listed in `G` contain N/A, the N/A value is considered a valid grouping value.
`S`	integer	The name of a column in which every row evaluates to a 1 or 0, which determines whether or not that row is selected to be included in the calculation If `S` is omitted, all rows will be considered by the function (subject to any prior row selections). If any of the values in `S` are neither 1 nor 0, an error is returned.
`X`	any simple type	`X` is a column of node IDs. A column name
`Y`	any simple type	`Y` is a column of pointers to the next node ID (out of `X`) in a directed graph. Note: Trees are a subset of directed graphs. A column name
`K`	integer	The name of a column that contains a 1 or 0 value, indicating the initial selection of nodes If any of the values in `K` are neither 1 nor 0, an error is returned.
`D`	integer or text	A value that determines the behavior of the function `D` can either be an integer or one of the following string values: `'all'` - all nodes that are reachable from the initial selection of nodes `'leaf'` - all leaf nodes that are reachable from the initial selection of nodes `'depth'` - the least amount of hops from the initial selection of nodes If `D` is omitted, the default behavior is the same as `'all'`.

Return Value

For every row in each group defined by G (and for those rows where S=1, if specified), g_chase returns an integer value:

If D is 'all', then the result is 1 for all nodes that are reachable by any number of hops from the initial selection, which includes:
- the initial set of rows R0 where K is 1
- the set of rows R1 that are pointed to by the initial set R0 (i.e., those rows where X is found in the values of Y at R0)
- the set of rows R2 that are pointed to by R1
- and so on ad infinitum
Otherwise, it returns a 0.
If D is 'leaf', then the result is 1 for all leaf nodes that are reachable by any number of hops from the initial selection (i.e., it is effectively negative infinity).
If D is 'depth', then the result for each row is the value corresponding to the least number of hops necessary to reach that row from the initial selection, or N/A if the row is not reachable.
If D is a non-negative integer X, then the result is 1 only for the union of R0, R1, ... RX (i.e., for all nodes that are reachable by no more than X hops away from the initial selection).
If D is a negative integer -X, then the result is 1 only for those rows in the union of R0, R1, ... RX that do not point to any subsequent rows (i.e., only for the leaf nodes that are at most X hops away from the initial selection).
If D is 0, then trivially the function is equal to K.

Note: Cycles are detected and short-circuited (i.e., if the directed graph is not a tree and, for example, A points to B, which points to C, which points to A again, it won't run forever).

Example

g_chase(G;S;X;Y;K;D) is a fairly complex function that "chases" linked nodes in a hierarchy represented by two columns containing "parent" and "child" node IDs.

Consider the following organization chart:

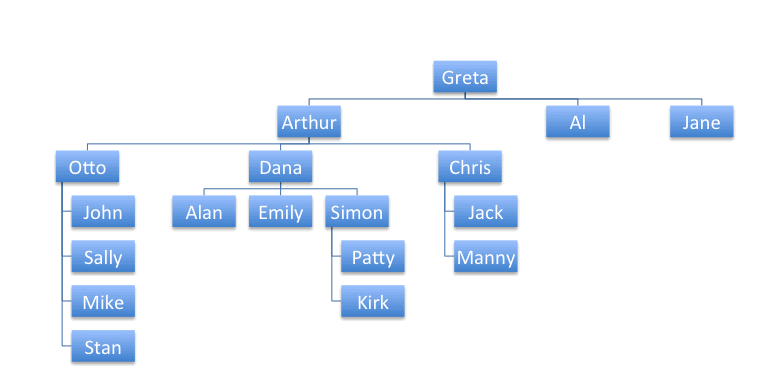
This chart can be represented by the following table:

Note: For this example, you can create a temporary version of this table using the <table> operation:

<table title="Org Chart" cols="supervisor,employee" labels="Supervisor,Employee">
Greta,Arthur;
Greta,Al;
Greta,Jane;
Arthur,Otto;
Arthur,Dana;
Arthur,Chris;
Otto,John;
Otto,Sally;
Otto,Mike;
Otto,Stan;
Dana,Alan;
Dana,Emily;
Dana,Simon;
Simon,Patty;
Simon,Kirk;
Chris,Jack;
Chris,Manny;
</table>

We can use g_chase(G;S;X;Y;K;D) to find all of the nodes under Arthur.

We'll omit the G parameter so that all rows will be considered to be in the same group, and we'll omit the S parameter since we want all rows to be considered by the function.

For our X parameter, we'll specify the supervisor column, and for the Y parameter, we'll specify the employee column. (In relation to the organization chart, each value in the supervisor column is the "parent" of the corresponding value in the employee column.)

For the K parameter, we need to specify a column that indicates the initial selection of nodes. So we'll create a computed column whose value is 1 for those rows where the supervisor column has the value 'Arthur':

<willbe name="top" value="supervisor='Arthur'"/>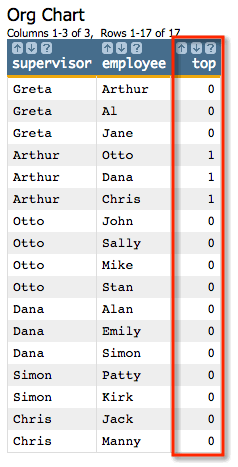

For the D parameter, we'll specify 'all' since we want to find all of the nodes under Arthur.

So our call to g_chase(G;S;X;Y;K;D) will look like:

<willbe name="all" value="g_chase(;;supervisor;employee;top;'all')"/>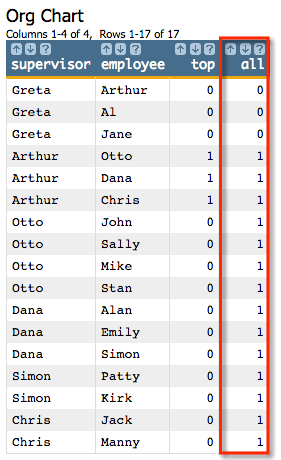

The all column contains a 1 for those nodes that are reachable by any number of hops from the initial selection. Note that the Greta node is not reachable from Arthur, so each of those rows contain a 0.

If we wanted to find all of the leaf nodes under Arthur, we would only have to change the D parameter to 'leaf':

<willbe name="leaf" value="g_chase(;;supervisor;employee;top;'leaf')"/>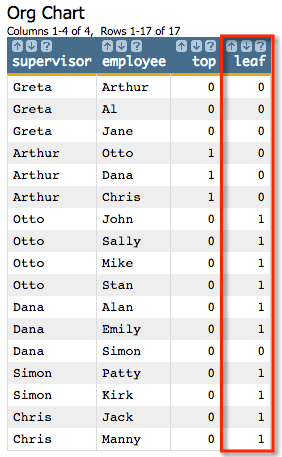

We can see that those rows where the leaf column contains a 1 are the rows that contain leaf nodes reachable by any number of hops from the initial selection. Note that the row where supervisor has the value Dana and employee has the value Simon contains the value 0 because Simon is not a leaf node.

To find out the least number of hops necessary to reach each row from the initial selection, we can change the D parameter to 'depth':

<willbe name="depth" value="g_chase(;;supervisor;employee;top;'depth')"/>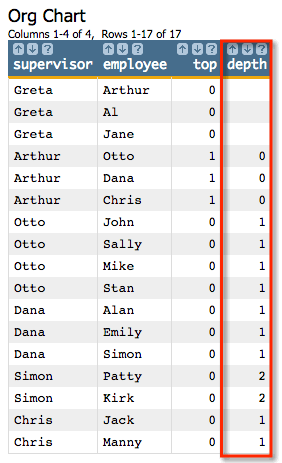

The results indicate that:

Arthur is 0 hops from Arthur
Otto is 1 hop from Arthur
Simon is 2 hops from Arthur

Because Greta is not reachable from Arthur, the result is N/A for those rows.