g_markov(G;S;O;T;H;D;M)

Returns the results of running a Monte Carlo Markov-chain simulation within a given group.

Syntax

g_markov(G;S;O;T;H;D;M)

Input

Argument Type Description
G any A space- or comma-separated list of column names

Rows are in the same group if their values for all of the columns listed in G are the same.

If G is omitted, all rows are considered to be in the same group.

If any of the columns listed in G contain N/A, the N/A value is considered a valid grouping value.
S integer The name of a column in which every row evaluates to a 1 or 0, which determines whether or not that row is selected to be included in the calculation

If S is omitted, all rows will be considered by the function (subject to any prior row selections).

If any of the values in S are neither 1 nor 0, an error is returned.
O integer A space- or comma-separated list of column names that determine the row order within a particular group

If O is omitted, the order is the current display order of the table.

If any of the values in O are N/A, an error is returned.
T integer A scalar value or the name of a column

T represents discrete time steps of the simulation.

If present, T must be (within each group) a non-decreasing sequence of integers greater than or equal to zero. For example: 1,2,3,4... or 0,1,4,5,5,6,7...
  • Contiguous values at each row represent single steps (e.g., 1,2,3)
  • Skipped values would lead to more than one step in the simulation (e.g., 1,4)
  • Repeated values would not step the simulation forward

If the sequence begins with 0, then the state at that row is the initial state (see H below). If the sequence begins with 1, then the state at that row is the result of the first transition from the initial state.

If T is omitted, it defaults to 1,2,3,4... for each group.
H integer A scalar value or the name of a column

H represents the initial state of the simulation for the group.

H must be an integer between and including [1 .. N], where N is the number of states (see description of M below).

If H is a column, it should be the same for all values in a group (only the first value will be used).
D integer A scalar value or the name of a column

D determines the random seed for the group.

If D is a column, it should be the same for all values in a group (only the first value will be used).
M decimal A space- or comma-separated list of either scalar values or column names

M represents a transition matrix (which can be non-stationary, to the extent that it has column elements).

M must have a square number of values, N*N, where N is the number of possible states.

For example, the list:

A1 A2 A3 B1 B2 B3 C1 C2 C3

represents the 3*3 matrix:

A1 A2 A3
B1 B2 B3
C1 C2 C3

The value in row I, column J is to be interpreted as the probability that state I will transition to state J. 

The values in each row should sum to 1.0 (if they do not, the result from g_markov will have little meaning).
Note: If T, H, D, and M are the same, then the result of g_markov will be the same (for the same number of rows).

Return Value

For every row in each group defined by G (and for those rows where S=1, if specified), g_markov returns an integer value corresponding to the state with respect to running a Monte Carlo Markov-chain simulation within that group, where the order of rows in the simulation is determined by O, if specified (otherwise, the order is the current display order of the table).

The simulation starts at a state H, and at each time step T, "the dice are rolled" and the next state is transitioned to with a probability determined by M. The result of the function for each row is the state at that row.

Example

Let's use the Weather Underground Observed Daily table (pub.demo.weather.wunderground.observed_daily) to illustrate the use of g_markov(G;S;O;T;H;D;M).

Let's say we want to perform a Monte Carlo Markov-chain simulation to generate random samples of weather conditions in a particular zip code. To do this, we'll need a transition matrix that consists of the probabilities of weather conditions for that zip code, specifically related to sunny vs. rainy days.

Our transition matrix should look something like:

probS_S probS_R
probR_S probR_R
where:
  • probS_S is the probability that it will be sunny tomorrow given that it is sunny today
  • probS_R is the probability that it will be rainy tomorrow given that it is sunny today
  • probR_S is the probability that it will be sunny tomorrow given that it is rainy today
  • probR_R is the probability that it will be rainy tomorrow given that it is rainy today

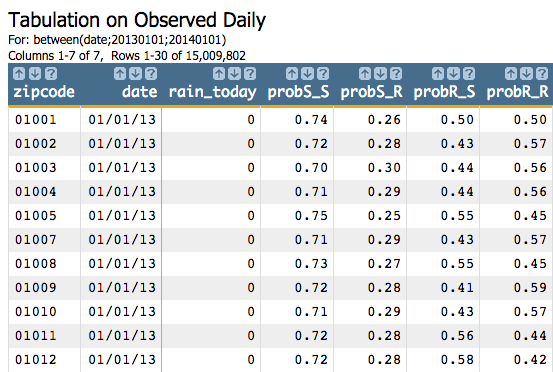
We can easily figure out this matrix from the data in the table by using the following Macro Language code:

<sel value="between(date;20130101;20140101)"/>
<tabu label="Tabulation on Observed Daily" breaks="zipcode,date">
  <break col="date" sort="up"/>
  <tcol source="rain" fun="hi" name="rain" label="Highest`Rain``"/>
</tabu>
<willbe name="rain_today" value="int(rain)"/>
<willbe name="sunny_today" value="~rain_today"/>
<willbe name="rain_tomorrow" value="g_rshift(zipcode;;;rain_today;1)"/>
<willbe name="probR_R" value="g_sum(zipcode;rain_today;rain_tomorrow)/g_sum(zipcode;;rain_today)" format="dec:2"/>
<willbe name="probR_S" value="1-probR_R" format="dec:2"/>
<willbe name="probS_R" value="g_sum(zipcode;sunny_today;rain_tomorrow)/g_sum(zipcode;;sunny_today)" format="dec:2"/>
<willbe name="probS_S" value="1-probS_R" format="dec:2"/>
<colord cols="zipcode,date,rain_today,probS_S,probS_R,probR_S,probR_R"/>

This will give us the following results:

For g_markov(G;S;O;T;H;D;M), we'll specify zipcode for the G parameter, since we want to run the simulation for each zip code. We'll omit the S parameter since we want the function to consider all rows and not just a subset, and we'll specify date for the O parameter to order the rows in the simulation by date.

We'll omit the T parameter, so that the result in each of the rows will represent a single step in the simulation.

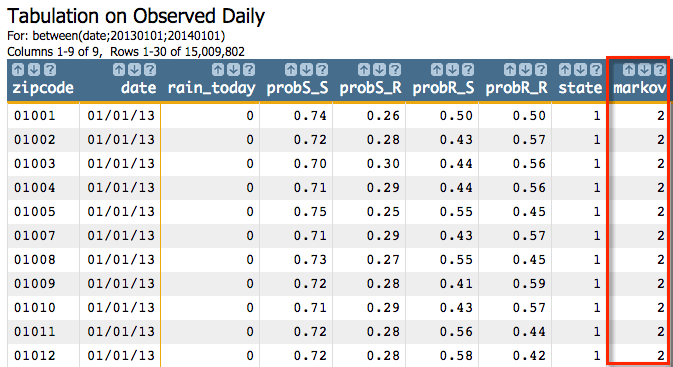
For the H parameter, we need to specify a start state, which can either be 1 (sunny) or 2 (rainy), so we'll create a state column we can use for that parameter:
<willbe name="state" value="rain_today+1"/>

For the D parameter, we need to specify an integer value that will determine the random seed for the group. For our example, we'll use the value 42, but this can be any integer value.

Finally, the M parameter would be the list of values from our transition matrix: probS_S probS_R probR_S probR_R.

So, our call to g_markov(G;S;O;T;H;D;M) would look like:
<willbe name="markov" value="g_markov(zipcode;;date;;state;42;probS_S probS_R probR_S probR_R)"/>

This gives us results similar to the following:

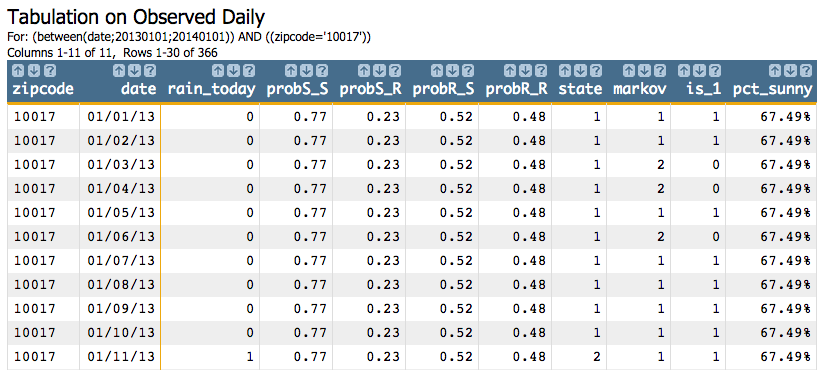
Let's look at the results for the zip code 10017:
<sel value="(zipcode='10017')"/>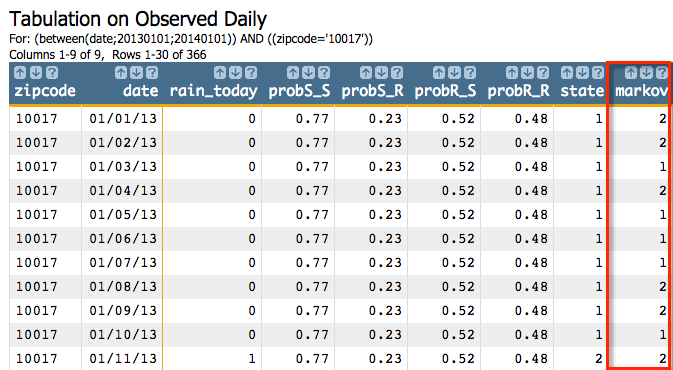

Since we ordered by the date column, the simulation will start at the row with the date 01/01/13, and the start state will be 1. The result from the first step of the simulation using the seed and the transition matrix we specified, is 2, which becomes the start state for the next step of the simulation. The result from that step is 2, and then 1, and so on for all 366 steps of the simulation.

If we wanted to see the percentage of sunny days predicted by this simulation, we could use the following Macro Language code:
<willbe name="is_1" value="markov=1"/>
<willbe name="pct_sunny" value="g_cnt(zipcode;is_1)/g_cnt(zipcode;)" format="type:pct;dec:2"/>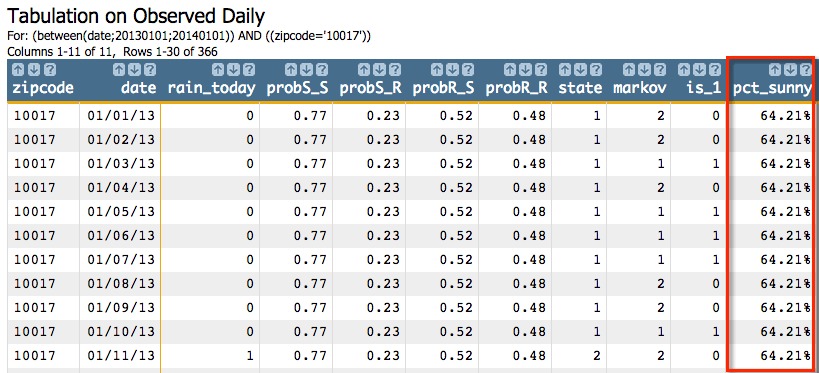

So we can see that 64.21% of the time in this simulation, g_markov predicted the weather would be sunny. If we ran the simulation with a different seed or ran it on a different zip code that had a different transition matrix, we would get slightly different results. For example, if we changed the seed to 38746 for the 10017 zip code, we would get the following results: